Wilcoxon Signed-Rank test Calculator

To calculate a Wilcoxon test (Wilcoxon signed-rank test) online simply select 2 metric variables or two ordinal variables.

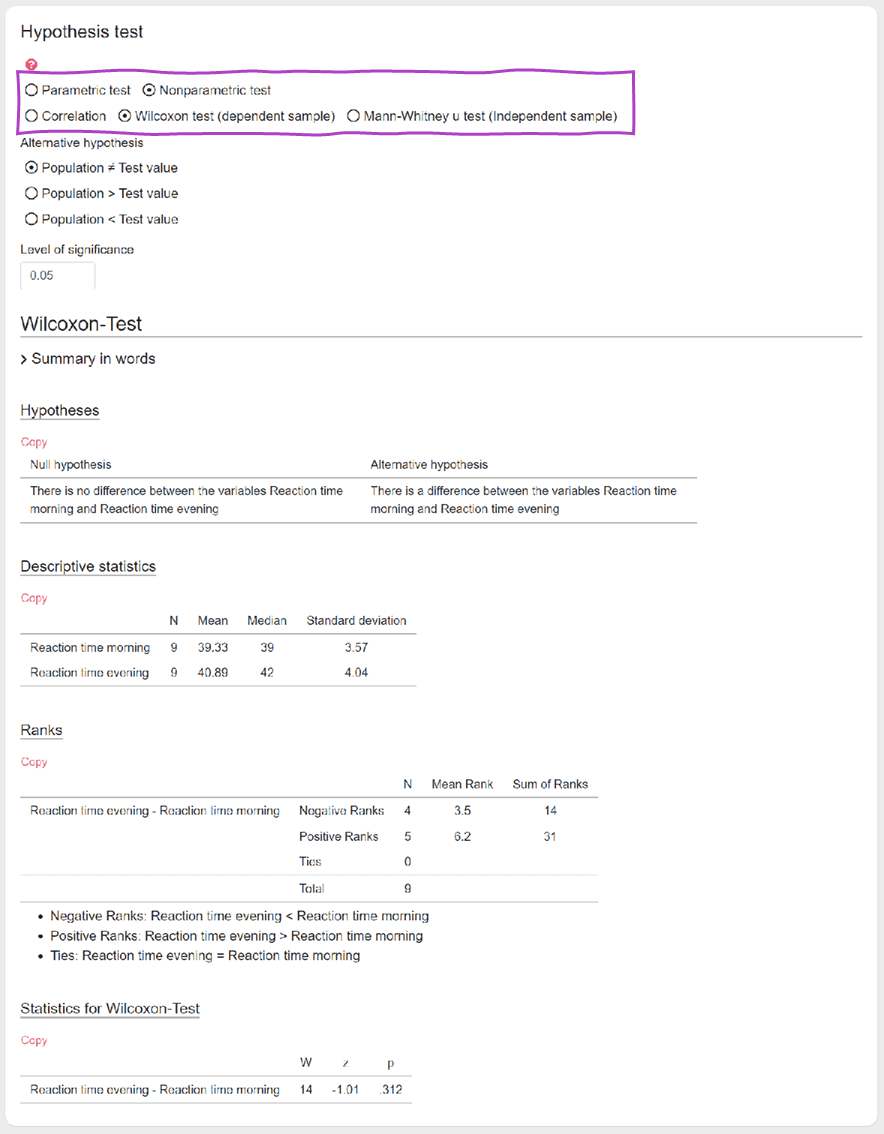
Afterwards the results of the Wilcoxon test will be displayed clearly. First you get the hypotheses of the Wilcoxon test and then the calculated rank sums and the p-value.

If you click on more than two metric or ordinal variables, a Friedman test is automatically calculated.

Wilcoxon Signed-Rank Test

The Wilcoxon Signed-Rank Test is a non-parametric statistical test that is used to compare two related samples, to determine whether their population mean ranks differ (i.e., it's used for paired data). It's an alternative to the paired t-test when the distributional assumptions of the t-test (like normality) are not met.

How the Wilcoxon Signed-Rank Test Works:

1. Differences: For each pair in the dataset, calculate the difference between the two observations.
2. Ranking: Rank the absolute values of these differences, ignoring any differences that are zero (because the sign of zero is not defined).
3. Signs: Assign each ranked difference its original sign (from step 1).
4. Sum of Ranks: Calculate the sum of the positive ranks (let's call it W ⁺) and the sum of the negative ranks (let's call it W ^-).
5. Test Statistic: The test statistic W is the smaller of W ⁺ and W ^-. In some variations, W might be defined as the larger of the two sums, depending on the table or software being used.
6. Determine Significance: To determine if the observed differences are statistically significant, you would compare W to a critical value from the Wilcoxon distribution (for small sample sizes, typically you'd use a table of critical values). For larger samples, the distribution of W can be approximated using a normal distribution, allowing for the computation of a p-value.

The Wilcoxon Signed-Rank Test makes fewer assumptions than the paired t-test, which assumes that the differences between the pairs follow a normal distribution. The Wilcoxon test only assumes that the data is ordinal (i.e., it can be ranked). It's particularly useful when dealing with skewed data or data with outliers.

However, note that while the Wilcoxon Signed-Rank Test can indicate whether there's a statistically significant difference between the groups, it doesn't indicate the magnitude or direction of the difference like the mean does in a t-test. Instead, it's based on the medians and ranks.

Reporting the results of the Wilcoxon Signed-Rank Test

When reporting the results of the Wilcoxon Signed-Rank Test according to APA (American Psychological Association) style, you should provide the relevant test statistic, the significance level, and any other pertinent information in a clear and concise manner.

1. Specify the Test and Purpose:
   • Clearly mention that you performed a Wilcoxon Signed-Rank Test and briefly explain the purpose of the test.
   • E.g., "A Wilcoxon Signed-Rank Test was conducted to assess..."
2. Report the Test Statistic:
   • State the Wilcoxon T statistic.
   • E.g., "T = 23,"
3. Report the Significance Level:
   • Clearly indicate the exact p-value obtained.
   • If the p-value is less than .001, you can report it as "p < .001."
   • If the p-value is, for example, .045, you would report it as "p = .045."
4. Sample Size:
   • Mention the number of pairs (or matched observations) used in the test.
   • E.g., "n = 30 pairs."
5. Effect Size (if calculated):
   • If you have calculated an effect size, report it and describe its magnitude.
   • E.g., "r = .40, indicating a medium effect size."
6. Summarize the Results:
   • After presenting the statistics, provide a summary sentence to highlight what the results mean in the context of your study.
   • E.g., "The test indicated a significant difference between the paired observations."

As with all APA-style reporting, clarity and conciseness are crucial. Your audience should be able to understand the statistical test you used, the key results, and the implications of these results easily.

Here's a comprehensive example:

"A Wilcoxon Signed-Rank Test was conducted to compare the pre-test and post-test scores of participants. The test indicated a significant difference between the paired observations, T = 23, n = 30 pairs, p = .045, with a medium effect size, r = .40."