Two-way ANOVA with repeated measures Calculator

If you want to calculate a two-way analysis of variance with repeated measures, simply select more than three metric variables and one nominal variable.

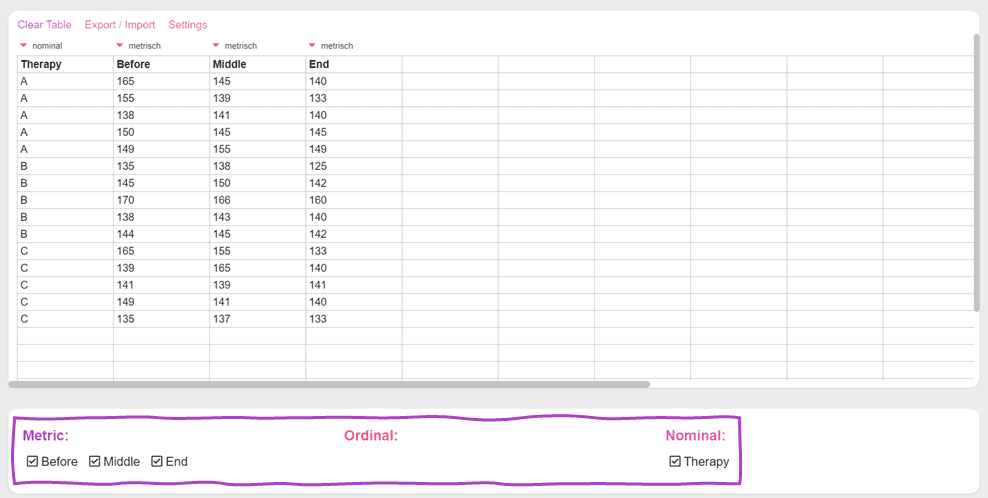
If both factors are independent, i.e. if there are no repeated measurements, you can calculate a two-factor analysis of variance online. If you have only one factor and it consists of repeated measures, calculate a one-factor analysis of variance with repeated measures.

Two-way ANOVA with repeated measures

A two-way ANOVA with repeated measures is a statistical technique used to analyze the effects of two independent variables (factors) on a dependent variable, where each participant or subject is measured multiple times under all combinations of the two factors. This design is commonly referred to as a "mixed-design" or "split-plot" design because it combines aspects of both between-subjects and within-subjects designs.

In a two-way ANOVA with repeated measures, there are two main factors, Factor A and Factor B, and the same participants are exposed to all levels of both factors. The goal is to examine whether there are main effects of each factor (Factor A and Factor B) and whether there is an interaction effect between the two factors on the dependent variable.

Here's a breakdown of the factors and their levels:

• Factor A: The first independent variable with 'a' levels or conditions.
• Factor B: The second independent variable with 'b' levels or conditions.

The basic steps of conducting a two-way ANOVA with repeated measures are as follows:

• Define the research question: Determine the variables, the specific levels of each factor, and the interactions to be investigated.
• Collect data: Measure the dependent variable(s) for each participant under all combinations of Factor A and Factor B.
• Perform the ANOVA: Analyze the data using a two-way repeated measures ANOVA to assess main effects and interactions.
• Check assumptions: Ensure that the data meet the assumptions of the test, such as normality and sphericity (homogeneity of variances of the differences between all pairs of conditions).
• Interpret the results: Examine the main effects of Factor A and Factor B and determine whether there is a significant interaction effect between the two factors.
• Post hoc tests (if necessary): If an interaction effect is significant, further post hoc analyses may be performed to explore specific differences between individual conditions.
• Report the findings: Present the results, including effect sizes and any relevant post hoc analyses, in a clear and concise manner.

A two-way ANOVA with repeated measures is a powerful design because it allows researchers to investigate the main effects of each factor and their combined effect on the dependent variable, while also benefiting from increased statistical power due to the repeated measures aspect. However, as with any statistical analysis, researchers should be cautious about assumptions and potential biases to ensure the validity of their findings.