Friedman-Test Calculator

To calculate a Friedman test online, simply select 3 or more metric variables or 3 or more ordinal variables and click on non-parametric test.

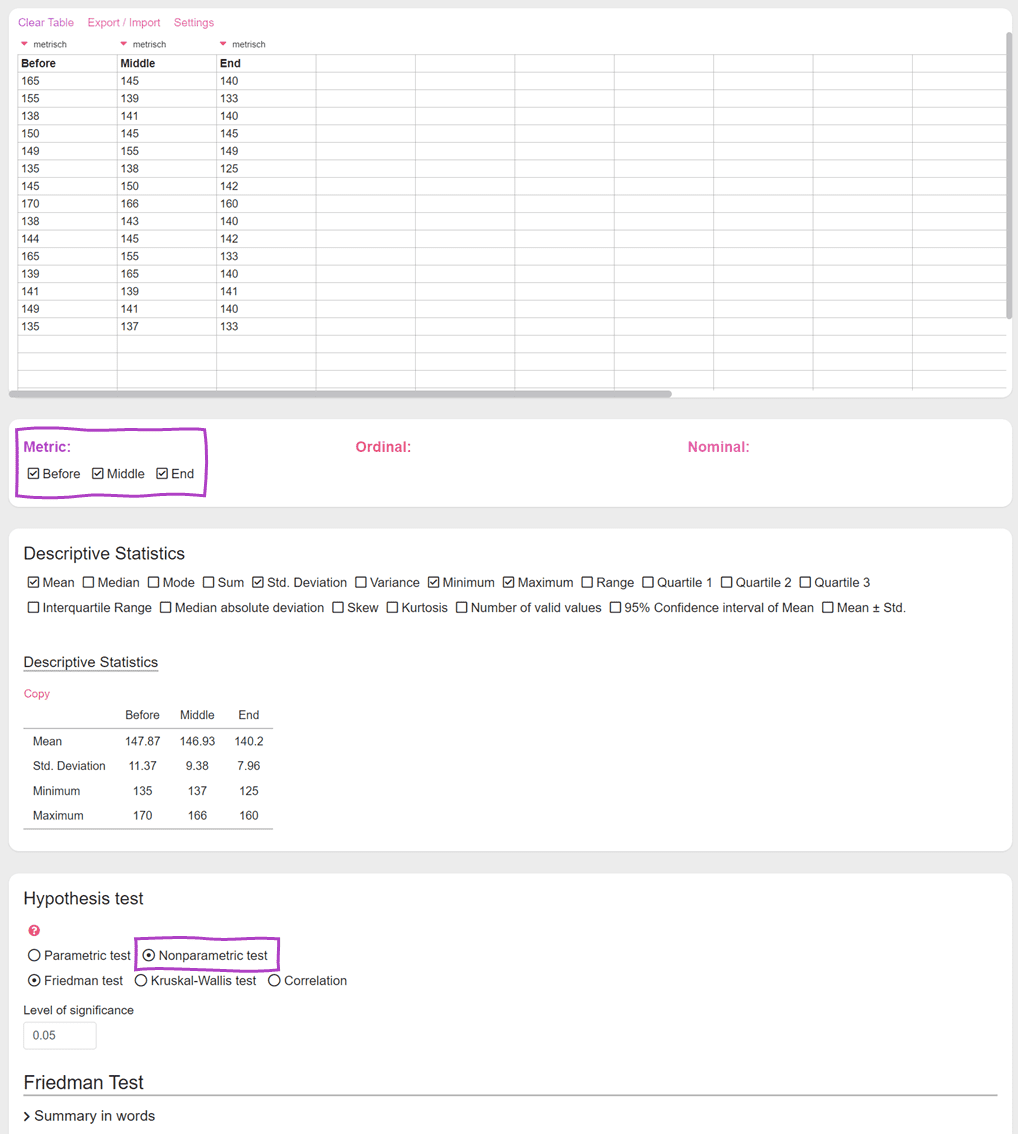
Friedman Test

The Friedman Test is a non-parametric statistical test used to compare the means of three or more paired groups. It's essentially an extension of the Wilcoxon Signed-Rank Test to handle more than two related groups. The Friedman Test is often used in cases where you have repeated measures on the same subjects (e.g., measuring a response at multiple time points or under different conditions).

The test is named after the statistician Milton Friedman, and it is useful for analyzing randomized block designs. The Friedman test is the non-parametric counterpart to repeated measures ANOVA. If you do not have a dependent random sample, you can also use the Kruskal-Wallis Test Calculator

Basic Breakdown of the Friedman Test:

1. Ranking: For each block (which could be, for instance, an individual subject in a repeated measures design), rank the data from 1 to k (where k is the number of groups). If there are ties, average ranks are given.
2. Rank Sums: Calculate the sum of ranks for each group across all blocks.
3. Test Statistic Calculation: The Friedman test statistic chi ² is computed based on the sum of ranks, number of blocks, and number of groups. The formula involves summing the squared rank sums, multiplying by certain constants, and subtracting corrections to get the chi ² value.
4. Determine Significance: The test statistic chi ² is compared to a chi-squared distribution with k-1 degrees of freedom (where k is the number of groups) to determine if the observed differences between the groups are statistically significant.
5. Post-Hoc Analysis: If the Friedman test is significant, it indicates that at least two groups have different means, but it doesn't specify which groups differ from each other. To determine pairwise differences, post-hoc tests (like the Nemenyi test or pairwise comparisons using the Wilcoxon Signed-Rank Test with a correction for multiple comparisons) can be performed.

Hypotheses for the Friedman test

For the Friedman test, the hypotheses are:

• Null Hypothesis (H0): The distributions of the rankings for each treatment are the same. In other words, there are no differences in the treatments over the repeated measures or blocks.
• Alternative Hypothesis (H1): At least two treatments have different distributions of the rankings. This implies that there is a difference in at least one of the treatments over the repeated measures or blocks.

To determine whether the null hypothesis should be rejected, the test calculates a test statistic, which is then compared with a critical value from the chi-squared distribution (χ2), or a p-value is calculated and tested if it is less than the specified significance level. If the test statistic is sufficiently large, the null hypothesis is rejected, meaning that there are significant differences between treatments.

Key Points:

• The Friedman Test is non-parametric and doesn't make assumptions about the distributions of the data.
• It works with ranked data, so it's appropriate for ordinal or non-normally distributed interval data.
• The test is designed for paired data from related groups, making it ideal for repeated measures or within-subjects designs.

Like with other statistical tests, the result should be interpreted in the context of the study, considering both statistical significance and practical implications.