Kruskal-Wallis Test Calculator

To calculate a Kruskal-Wallis test online, copy your data into the above table and simply select one metric or one ordinal variable and one nominal variable with at least 3 categories.

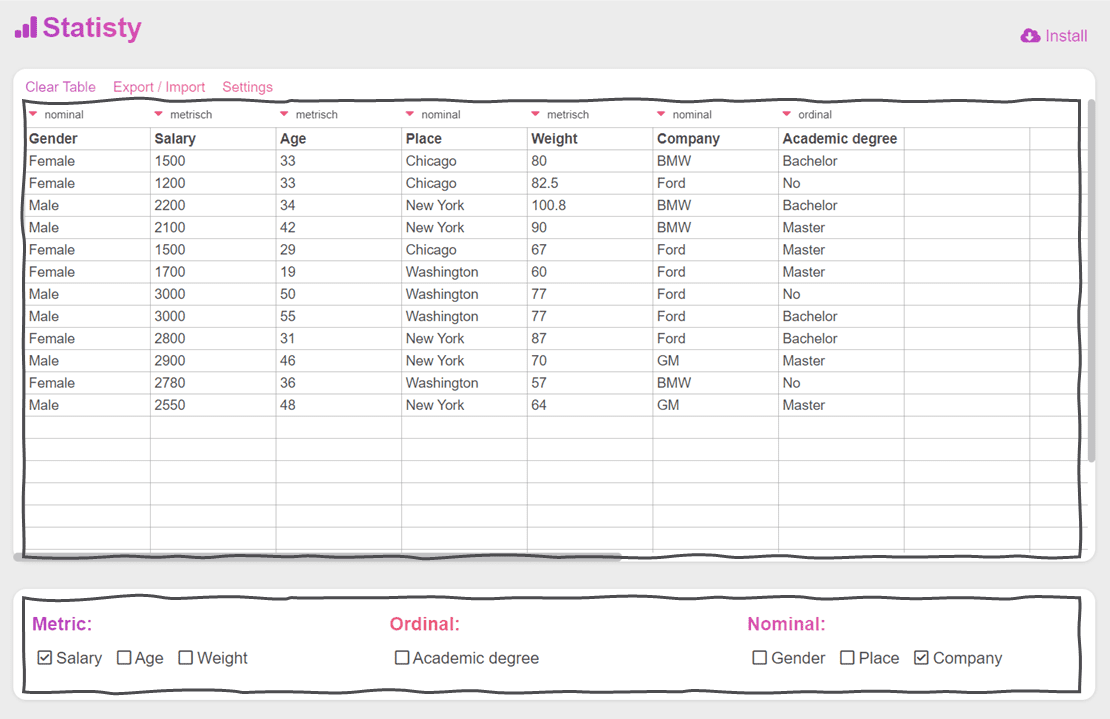
Then click on non-parametric and you will get the results of the calculated Kruskal-Wallis test.

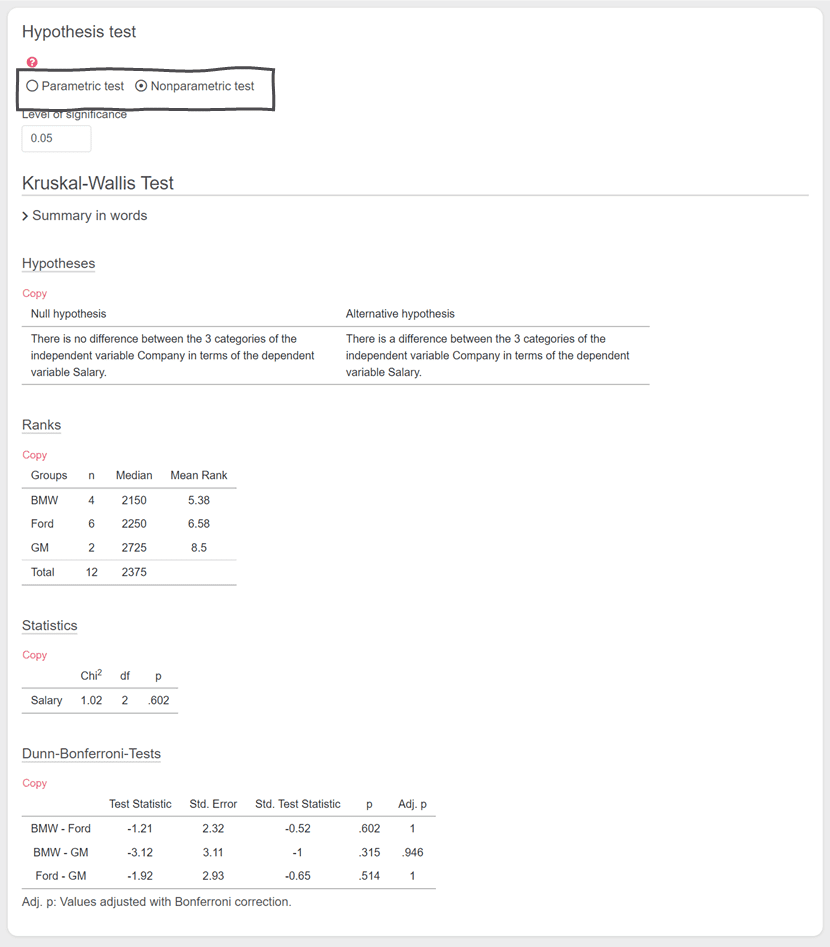
If your nominal variable has only two values, a Mann-Whitney u test is automatically calculated.

Kruskal-Wallis Test

The Kruskal-Wallis test is a non-parametric statistical test that is used to determine if there are statistically significant differences between two or more groups of an independent variable on a continuous or ordinal dependent variable. Essentially, it's the non-parametric version of the one-way analysis of variance (ANOVA). It is named after William Kruskal and W. Allen Wallis, who introduced the test.

The test is useful when the assumptions of ANOVA are not met, especially when the data doesn't meet the criteria for normality or when the homogeneity of variances is violated.

Basic Outline of the Kruskal-Wallis Test:

1. Ranking: All the data from the different groups are combined and ranked together. The smallest number gets the rank of 1, the next smallest number gets a rank of 2, and so on. In case of ties (equal values), average ranks are given.
2. Group Ranks Summation: The ranks for each group are then summed separately.
3. Test Statistic Calculation: The test statistic H is calculated using the formula, which involves the number of observations, the rank sums, and some correction factors. The equation for H can get a bit involved, but it essentially helps to compare the observed rank sums to what we would expect under the null hypothesis (that all groups have the same distribution).
4. Determine Significance: The test statistic H is then compared to a chi-squared distribution to determine if the observed differences between the groups are statistically significant. If the H value is sufficiently large, this would lead to the rejection of the null hypothesis, suggesting that at least one group's median is different from the others.
5. Post-Hoc Analysis: If the Kruskal-Wallis test is significant, it only indicates that at least two groups are different, but it doesn't specify which groups differ from each other. For this purpose, post-hoc tests (like the Dunn's test) can be used to make pairwise comparisons between groups.

Important Points:

• The Kruskal-Wallis test doesn't assume normality of the data but does assume that all groups have the same shape of distribution.
• The test is based on ranks, and thus the actual values of data are not as crucial as their relative rankings.
• While the test can determine if there are differences between groups, it doesn't indicate the magnitude or direction of differences.

When interpreting results, as with all statistical tests, it's crucial to consider the practical significance of findings, not just the statistical significance.