Two-way ANOVA Calculator

If you want to calculate a two-way ANOVA (two-factor ANOVA), simply select one metric variable and two nominal variables.

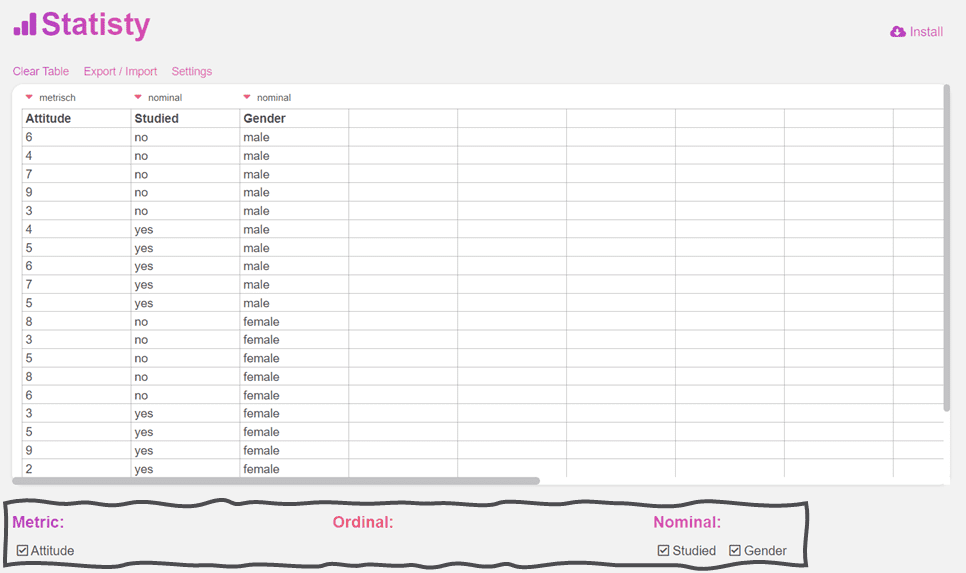
The results of the calculated two-factor analysis of variance are then clearly presented.

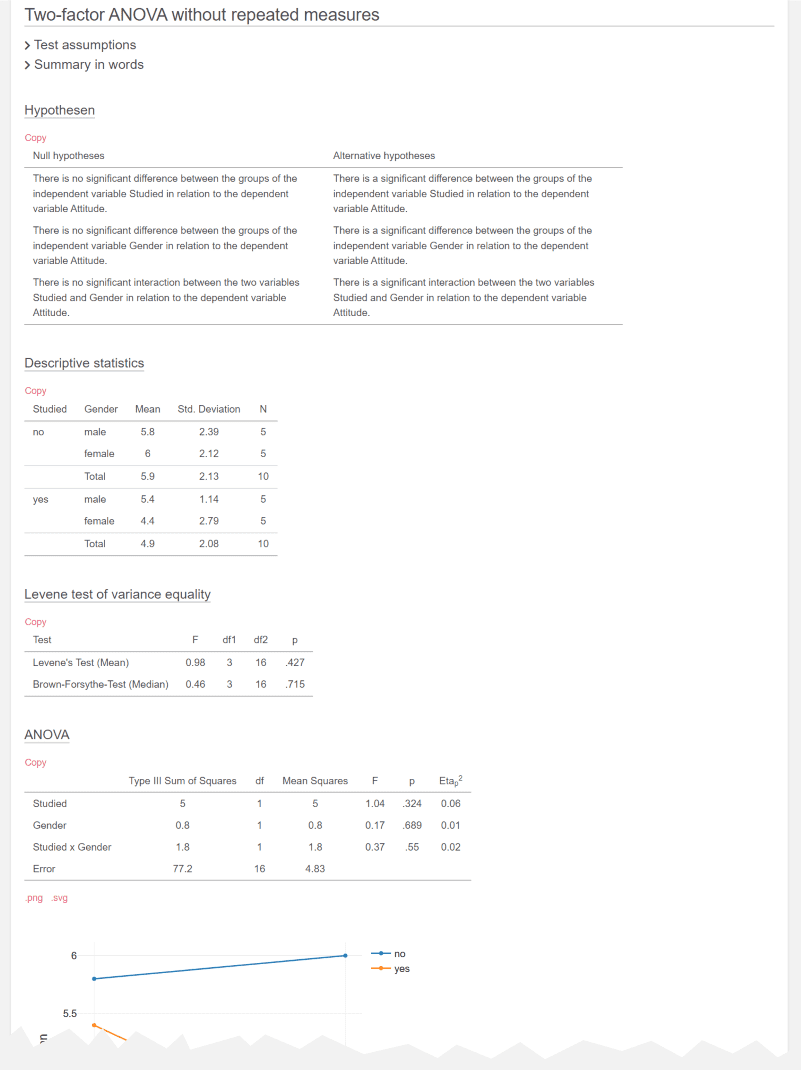
If you select a metric variable and a nominal variable with more than two categories, a one-way analysis of variance will be calculated.

Two-way ANOVA

A two-way ANOVA (Analysis of Variance) is a statistical method used to analyze the effects of two independent categorical variables (factors) on a continuous dependent variable. It allows researchers to simultaneously examine the main effects of each factor and their interaction effect.

In a two-way ANOVA, there are two factors, and each factor has two or more levels or categories. The main goal is to determine if there are significant differences in the means of the dependent variable across different combinations of factor levels.

For example, imagine a study investigating the effect of two factors, such as "Gender" (with levels: Male and Female) and "Treatment" (with levels: A, B, and C), on a response variable, say, "Test Score." The two-way ANOVA will assess whether the mean test scores differ between genders, between different treatments, and whether there is an interaction effect between gender and treatment (i.e., whether the effect of treatment on test scores differs between genders).

The assumptions for performing a two-way ANOVA are similar to those of the one-way ANOVA:

• Independence: Observations are independent of each other.
• Normality: The data within each combination of factors are normally distributed.
• Homogeneity of variance: The variability (variance) of the data is approximately the same across all combinations of factors.

The output of a two-way ANOVA provides several key pieces of information, including:

• Main effects: Whether there are significant differences in the dependent variable due to each factor independently.
• Interaction effect: Whether there is a significant combined effect of the two factors that is not explained by their main effects alone.
• F-statistics and p-values: To assess the significance of the main effects and interaction effect.

If the two-way ANOVA indicates significant effects, post hoc tests can be conducted to identify specific differences between factor levels. Tukey's post hoc test or Bonferroni correction are commonly used for this purpose.